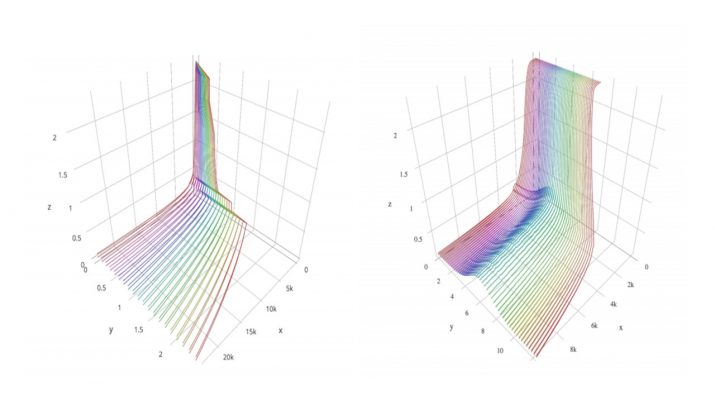
Given a (piece-wise) differentiable loss function, and a gradient-based algorithm to minimize it, the knowledge of the second-order information about it can tell us quite a bit about how the landscape looks like, and how we could modify our algorithm to make it go faster and find better solutions.
But, one of the biggest challenges in second-order optimization methods is in accessing that second-order information itself. In particular, in deep learning, there have been many proposals to accelerate training using second-order information. Ngiam et al. (2011) have an in-depth review of some of the proposals for approximating the Hessian of the loss function. Nevertheless, given the computational complexity of the problems at hand, we don’t have much information on what the actual Hessian looks like. This work is part of a series of papers that explore the data-model-algorithm connection along with Sagun et al. (2014; 2015) and it builds on top of the intuition developed in LeCun et al. (2012).
ABSTRACT
We look at the eigenvalues of the Hessian of a loss function before and after training. The eigenvalue distribution is seen to be composed of two parts, the bulk which is concentrated around zero, and the edges which are scattered away from zero. We present empirical evidence for the bulk indicating how over parametrized the system is, and for the edges indicating the complexity of the input data.
Levent Sagun, Leon Bottou, Yann LeCun